Exponent
| Expression | Meaning | Result | Explanation |
|---|---|---|---|
| \(2^3\) | \(2 \times 2 \times 2\) | 8 | Multiply 2 three times |
| \(5^2\) | \(5 \times 5\) | 25 | Square of 5 |
| \(10^0\) | — | 1 | Any non-zero number to the 0 power is 1 |
| \(2^{-3}\) | \(\frac{1}{2^3} = \frac{1}{8}\) | 0.125 | Negative = reciprocal |
| \(4^{-1}\) | \(\frac{1}{4}\) | 0.25 | Negative exponent = 1 over base |
| \(9^{1/2}\) | \(\sqrt{9}\) | 3 | Fractional = root |
| \(27^{1/3}\) | \(\sqrt[3]{27}\) | 3 | Cube root |
| \(16^{3/4}\) | \(\left(\sqrt[4]{16}\right)^3\) | 8 | Root first, then power |
Negative Exponents
Represents the reciprocal (1 divided by the base raised to a positive power) For example: \(2^{-3}\) = 0.125
Fractional Exponents
Represents roots. For example Cube root: \(\sqrt[3]{27}\) = 3
Logarithm
A logarithm is the inverse of an exponent.
\[\log_b(y) = x \quad \text{means} \quad b^x = y\]-
b= base -
x= exponent -
y= result
For Example:
\[\log_2(8) = 3 \quad \text{because} \quad 2^3 = 8\]Common Logarithm Types
| Notation | Name | Base |
|---|---|---|
log | Common logarithm | 10 |
ln | Natural logarithm | e ≈ 2.718 |
log₂, log₁₀, etc. | Custom base logarithm | any base |
root vs logarithm
- A root asks: “What number, when raised to a certain power (like 2 or 3), gives this result?”
- A logarithm asks: “To what power must I raise a base to get this number?”
| Concept | Root (√) | Logarithm (log) |
|---|---|---|
| Question it asks | What number to raise to n? | What power gives this number? |
| Example | \(\sqrt{16} = 4 → 4^2 = 16\) | \(\log_2(16) = 4 → 2^4 = 16\) |
| Fixed part | The power (e.g., square = 2) | The base (e.g., base 2 or base 10) |
| Output | The number itself | The exponent |
- A root finds the base, given the result and the power
- A logarithm finds the exponent, given the base and the result
Logistic function
There’s a family of functions called logistic functions whose output represents a probability, always outputting a value between 0 and 1. The standard logistic function, also known as the sigmoid function (sigmoid means “s-shaped”), has the formula:
\[f(x) = \frac{1}{1 + e^{-x}}\]- The ‘e’ is Euler’s number, a fundamental mathematical constant.
e≈2.71828... - Logistic functions is one of The most important exponential function.
Here are the classic corresponding graph of the sigmoid function:
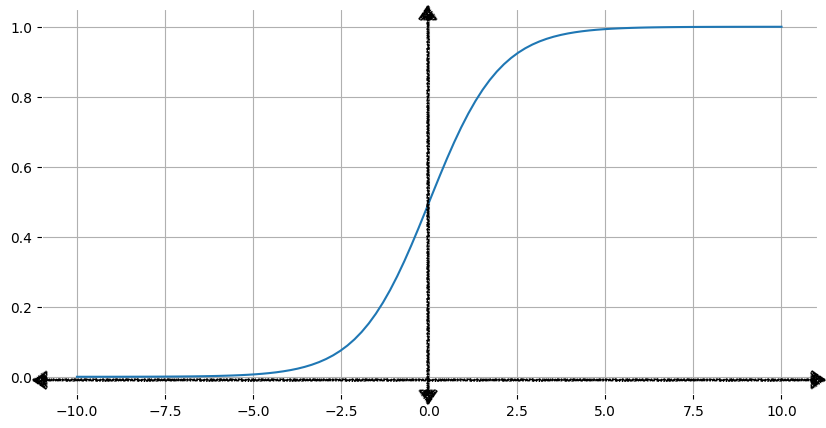
- As the input, x, increases, the output of the sigmoid function approaches but never reaches 1.
- Similarly, as the input decreases, the sigmoid function’s output approaches but never reaches 0.
- The sigmoid function will bend the linear equation straight line into an s-shape.
Quantile
What Is a Quantile? A quantile is a statistical term that refers to dividing a dataset into equal-sized intervals based on the values in the data. Quantiles help us understand the distribution of data and where values fall in relation to the whole set.
✅ Basic Idea Quantiles split data into parts of equal probability. For example:
- If you divide data into 4 parts, you get quartiles
- If you divide it into 100 parts, you get percentiles
- If you divide it into 10 parts, you get deciles